A little while ago, I wrote about the importance of understanding the difference between causation and correlation, and how the failure to do so could potentially be problematic for the management of your PPC accounts.
Sometimes when having the causation versus correlation conversation, the erroneous takeaway is this: correlating relationships are not actionable, only causal relationships are.
This statement isn’t true.
It’s important to understand that the presence of a relationship between data points does not necessarily mean that one data point caused the other data point’s behavior. But just because correlation doesn’t imply causation does not mean it can’t lead to action or insights.
In fact, identifying instances of correlation in your paid search accounts is a tremendous method for determining new tests.
And lucky for you, Microsoft Excel provides you a powerful function with which you can parse all of your data in one fell swoop. Pull out your data mining goggles, pickaxes, and headlamps. Time to hop down the shaft.
Here’s your primary tool:
=correl(
Powerful little sucker. The full nomenclature is as follows, with “A:A” representing your first data set, and “B:B” representing your second data set.
=correl(A:A,B:B)
This function tells Excel to compute the strength of the relationship between Data Set A and Data Set B. The strength of the relationship is presented as a decimal, called the correlation coefficient.
From Wikipedia:
“The Pearson product-moment correlation coefficient (sometimes referred to as the PPMCC or PCC or Pearson’s r) is a measure of the linear correlation (dependence) between two variables X and Y, giving a value between +1 and ?1 inclusive, where 1 is total positive correlation, 0 is no correlation, and ?1 is total negative correlation. It is widely used in the sciences as a measure of the degree of linear dependence between two variables. It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s.”
Long story short: the closer your correlation coefficient is to 1, the stronger the relationship. The closer it is to -1, the stronger the negative relationship (two metrics moving in opposite directions, such as conversions going up resulting in CPAs going down).
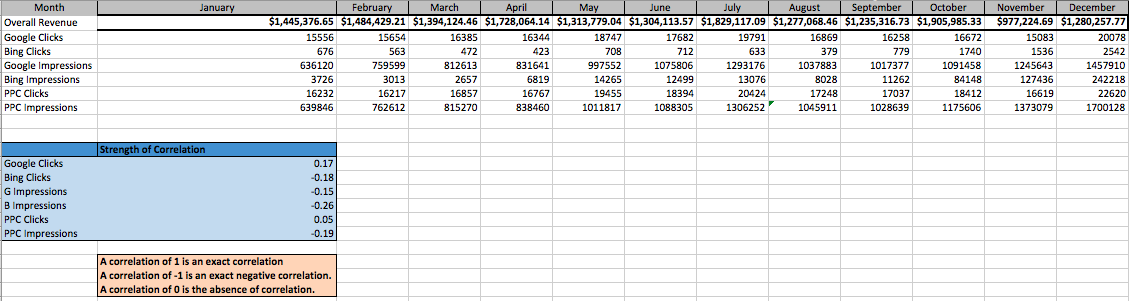
Here’s an example of how you might apply the correlation function to search for strong relationships in your account. Below, I’m attempting to quantify the relationship between a business’s digital presence, with their total revenue.
You can see that my approach was to pull in data for clicks and impressions in both Google and Bing, and then to aggregate those into “total PPC” metrics as well, to quantify overall paid digital efforts.
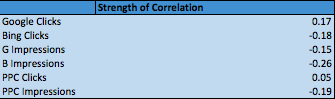
As you can see in the “Strength of Correlation” segment, none of these metrics had a significant relationship with the business’s overall revenue as all of their correlation coefficients were closer to zero than either one or negative one.
This is of course a very high-level look at the relationship between digital presence and total revenue. I was painting with broad strokes here, but the correlation function is a great lens to get more granular with your analysis as well.
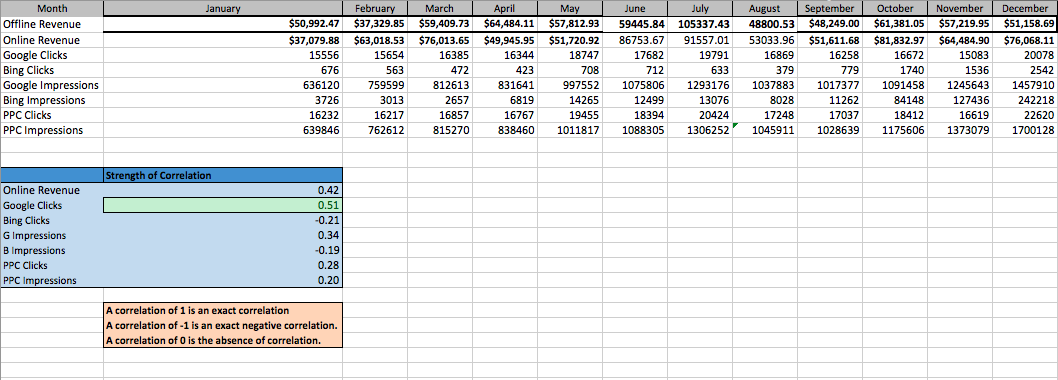
In the following example, I zoomed in just a little bit. I used the same metrics— clicks and impressions across both Google and Bing— but this time I checked their relationship with offline revenue (provided to me by the client).
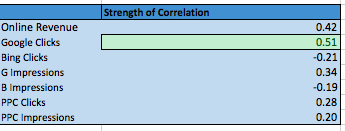
For the most part the relationships continued to err on the side of nonexistent. Google Clicks, however, crept up over that .50 mark. Sure, it’s a positive correlation of .51, but that’s closer to an exact correlation (1) than to no correlation (0).
Ultimately, with something like this, I’m not going to make any in-account changes, but I am going to keep an eye on the relationship between offline revenue and Google clicks, and study its fluctuations.
The above is an example where I used Excel’s correlation function to understand that there is no strong relationship between digital presence and overall revenue (apart from what I can already discern by looking at paid search revenue in a vacuum).
But I’ve also seen this function reveal some sneaky strong relationships. For example, in a different account, I took a look to see what sort of top-level performance metrics were possibly impacting the performance of my branded campaigns.
As it turns out, clicks that came in through our Google Display campaigns correlated noticeably with branded conversions. Advertising on the Display Network is commonly employed as a strategy for driving brand awareness. The correlation function quantitatively enforces that notion.
So What?
The premiere challenge in digital marketing is the vast array of moving parts behind the performance. It can be pretty difficult to understand the why. The measurables— arguably the premiere benefit of digital marketing— show us what happened. Not how it happened.
The correlation function can help us scan our accounts for these how and why moments, and they can provide insights in seconds that would take ages to arrive at manually (and for which we’d have the quantitative support).
Remember, nothing here is cut and dry. Correlations are not always causal. It’s very possible that your correlation is a coincidence, and that it’s not the how or why at all. But it’s also possible that it is, and that makes it worth knowing.
(featured image by Leo Grübler / Flickr)